Legt man den Laminat-Aufbau eines Faserverbund-Bauteils fest, sollte man stets an die anisotropen Eigenschaften der Verstärkungsfasern denken. Das bedeutet, dass die Festigkeit und Steifigkeit sehr stark von der Orientierung der Fasern zur Lastrichtung abhängen.
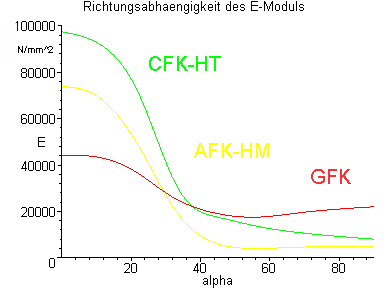
Zur Verdeutlichung sei hier ein Diagramm aus dem Buch "GFK-Technik im Modellbau" gezeigt: (S. 96, Daten für symmetrische Laminate, bei RT, Fasergehalt 60%)
Dieser Belastungsfall findet sich z.B. bei Rohren aus Flechtschlauch oder Belastung eines 0/90°-Gewebes in 45°-Richtung.
Was besonders deutlich hervortritt, ist die wesentlich größere Orientierungsempfindlichkeit der synthetischen Fasern gegenüber Glasfasern. Ihr Einsatz lohnt sich evtl. nur, wenn die genaue Belastungsrichtung bekannt ist (z.B. Holmgurte).
Auch sind die Festigkeit
und der E-Modul bei Zug- und Druckbelastung mitunter sehr unterschiedlich. Die
Glasfasern zeigen hier wegen ihres relativ großen Durchmessers von ca.
10 Mikrometern und ihres isotropen Molekülaufbaus (amorph) noch die geringsten
Unterschiede. HT-Carbonfasern (high tension) haben nur 7e-6 m Durchmesser, IM-Carbonfasern
(intermediate modulus) gar nur ca. 5,5. Dadurch ist die Einzelfaser trotz des
hohen E-Moduls relativ biegeweich. Bei Druckbelastung kommt es dann eher zum
Ausknicken der Fasern in der Matrix, d.h. Versagen.
Bei Zugbelastung
sind IM-Fasern den HT-Fasern deutlich überlegen. Der E-Modul eines UD-Laminates
in 0°-Richtung liegt hier bei ca. 180 GPa, die Zugfestigkeit bei ca. 2000-3000
MPa. HT-Fasern kommen bei Zug nur auf Werte von 144 GPa und ca. 1000-2000 MPa
Festigkeit. Bei der Druckfestigkeit sind aber HT- und IM-Fasern in etwa gleich
gut.
Wer sich über den großen Schwankungsbereich wundert - die Festigkeit
hängt sehr stark von der Ausrichtung der Fasern im Bauteil ab. Wellenbildung
bewirkt, dass die gerade verlaufenden Fasern zuerst die Last aufnehmen, während
sich die anderen ausrichten. Ihr Bruch zieht dann meist den Bruch des gesamten
Laminats nach sich.
Besonders groß sind
die Unterschiede zwischen Zug und Druck wieder bei Aramid-Fasern. Die Druckfestigkeit
beträgt i.a. nur 25% der Zugfestigkeit. Außerdem verformen sich Aramidfasern
auch bei Zugbelastung ab ca. 1,6% Dehnung plastisch.
Das Fazit aus diesen Feststellungen kann nur lauten: Aramid ist höchstens
dort einsetzbar, wo es auf maximale "impact restistance" ankommt,
also vielleicht Rümpfe. Diese brechen dann nicht, sondern knittern nur,
was sich notdürftig recht schnell reparieren lässt.
Die sich aus dem geringen spezifischen Gewicht von ca. 1,3 g/cm³ ergebende
größere Laminatdicke kommt vor allem der Beulsteifigkeit zugute,
so dass sich evtl. größere Durchmesser realisieren lassen. Wie hinlänglich
bekannt ist, wirkt sich das sehr positiv auf die Steifigkeit aus.
Da leichte Rümpfe i.a. durch Beulen versagen und die Druckfestigkeit des
Werkstoffs nicht ausgenutzt wird, liegt hier ein gewisser Vorteil von Aramid.
Den Effekt der Festigkeitsminderung durch vorzeitige Brüche einzelner Fasern trifft man vor allem bei Hybridlaminaten an. Gegenüber der Verwendung nur einer Faserart sinkt die Festigkeit quasi immer ab.
Der E-Modul parallel zur Faserrichtung des Composites mit zwei Faserarten kann mit Hilfe der Mischungsregel berechnet werden. Dabei wird angenommen, dass Fasern nach dem Bruch keinen Einfluß auf den E-Modul mehr haben.
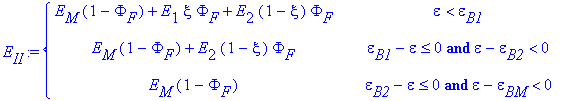
Dabei bedeuten 
,
,
die
Bruchdehnungen der beiden Faserarten und der Matrix (in aufsteigender Reihenfolge);
ist
der Anteil der Verstärkungsfasern und 
der
Anteil von Faser 1 am Faseranteil.
Die Mischungsregel besagt im Prinzip nichts anderes, als dass jeder Werkstoff entsprechend seinem prozentualen Anteil an der Querschnittsfläche zum Gesamt-E-Modul beiträgt.
Gemäß dem Hook'schen
Gesetz
kann
man nun die Zugspannung im Querschnitt berechnen. Dabei ergibt sich zum Beispiel
für ein Laminat aus HT-C-Fasern (30%) und HM-Aramidfasern (30%) in normalem
Epoxyd-Harz folgende Spannungs-Dehnungskurve:
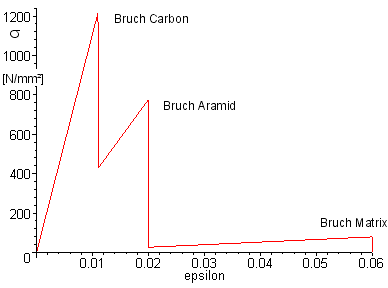
Nichtlinearitäten in den E-Moduli von Aramid-Fasern und Matrix sind hier
nicht mit berücksichtigt. Wenn die Dehnung nicht begrenzt ist (normalerweise
der Fall) bricht das Laminat natürlich schon mit dem Bruch der C-Fasern
vollständig.
Wie sich die Bruchspannung in Abhängigkeit vom Anteil der C-Fasern verhält, ist im folgenden Diagramm dargestellt.
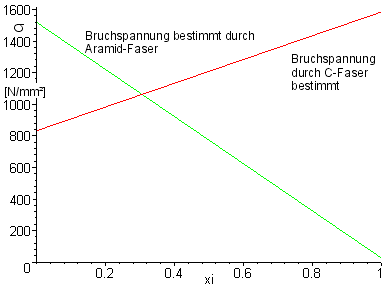
Wie man sieht, ergibt sich
bei einem Carbonanteil von ca. 30% ein Minimum in der Festigkeit des Laminats.
Die nach dem Bruch der C-Fasern verbleibenden Aramid-Fasern können wegen
des geringeren Querschnitts nicht mehr viel Belastung aufnehmen.
Das Diagramm gilt so nur für UD-Laminate, die Erkenntnisse lassen sich
aber sicher qualitativ auf mehrlagige Laminate unterschiedlicher Werkstoffe
übertragen.
to be continued...
Andreas, 06.01.2001